Adiabatic theory of strong-field ionization of molecules including nuclear motion: Rescattering
We extend the adiabatic theory of strong-field ionization of molecules including nuclear motion developed in our previous paper [J. Svensmark et al., Phys. Rev. A 101, 053422 (2020)] to describe rescattering processes. The adiabatic regime in which the electronic timescale is much smaller than that of the nuclei and laser field is considered. The asymptotics of rescattering parts of the solution to the time-dependent Schrödinger equation (TDSE) and ionization amplitude are obtained, and thus vibrationally resolved photoelectron momentum distributions (PEMDs) in the whole range of the photoelectron momentum are found. The ionization dynamics is described in terms of a nuclear wave packet in the molecular ion created as a result of ionization of the molecule, its evolution until rescattering, and a nuclear wave packet after rescattering. This complements the three-step model by accounting for what happens with the nuclear subsystem between ionization and rescattering events. A uniform asymptotics defining the PEMDs near a backward rescattering caustic is obtained, which enables one to extract the nuclear wave packet after rescattering from the PEMDs. The theory is illustrated by comparing its predictions with accurate numerical results obtained by solving the TDSE for a one-dimensional molecule with one electronic and one internuclear degree of freedom modeling H_2.
Adiabatic theory of strong-field ionization of molecules including nuclear motion
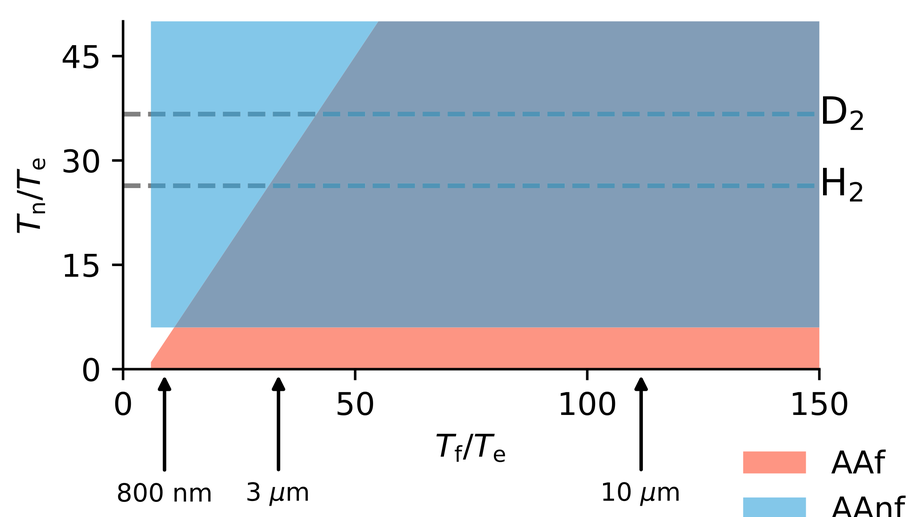
The adiabatic theory of strong-field ionization of molecules with internuclear motion included into consideration is developed. Two adiabatic regimes in terms of the electronic, nuclear, and laser field timescales are considered. In the first regime, field is the slowest; that is, its timescale is much larger than the electronic and nuclear timescales. The corresponding theory generalizes the adiabatic theory of strong-field ionization of atoms and molecules with frozen nuclei [Phys. Rev. A 86, 043417 (2012)] by treating the internuclear motion on equal footing with the electronic motion. In the second regime, the active electron is the fastest; that is, its timescale is much smaller than that of the nuclei and laser field. The corresponding theory naturally involves the Born-Oppenheimer approximation. The two versions of the adiabatic theory are validated by comparing their predictions with accurate numerical results obtained by solving the time-dependent Schrödinger equation (TDSE) for a model diatomic molecule with one electronic and one internuclear degree of freedom. The adiabatic results are shown to converge to the TDSE results uniformly with respect to the laser field amplitude both in tunneling and over-the-barrier ionization regimes. Two applications of the theory to the analysis of strong-field effects associated with the internuclear motion are discussed.
Bound and continuum energy distributions of nuclear fragments resulting from tunneling ionization of molecules
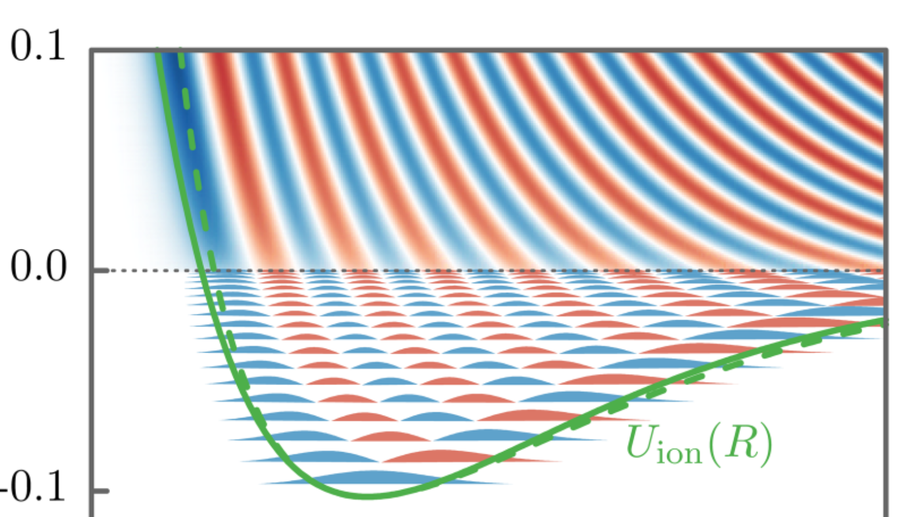
We present the theory of tunneling ionization of molecules with both electronic and nuclear motion treated quantum mechanically. The theory provides partial rates for ionization into the different final states of the molecular ion, including both bound vibrational and dissociative channels. The exact results obtained for a one-dimensional model of H2 and D2 are compared with two approximate approaches, the weak-field asymptotic theory and the Born-Oppenheimer approximation. The validity ranges and compatibility of the approaches are identified formally and illustrated by the calculations. The results quantify that at typical field strengths considered in strong-field physics, it is several orders of magnitude more likely to ionize into bound vibrational ionic channels than into the dissociative channel.
Tunneling Ionization of Diatomic Molecules
In this dissertation the theory of tunneling ionization of molecules is presented and the results of numerical calculations are shown.
Theory of dissociative tunneling ionization
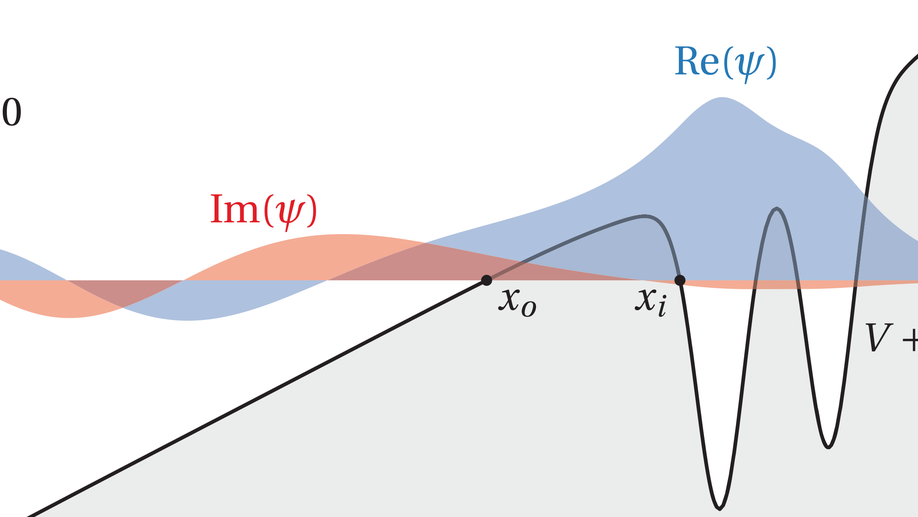
We present a theoretical study of the dissociative tunneling ionization process. Analytic expressions for the nuclear kinetic energy distribution of the ionization rates are derived. A particularly simple expression for the spectrum is found by using the Born-Oppenheimer (BO) approximation in conjunction with the reflection principle. These spectra are compared to exact non-BO ab initio spectra obtained through model calculations with a quantum mechanical treatment of both the electronic and nuclear degrees of freedom. In the regime where the BO approximation is applicable, imaging of the BO nuclear wave function is demonstrated to be possible through reverse use of the reflection principle, when accounting appropriately for the electronic ionization rate. A qualitative difference between the exact and BO wave functions in the asymptotic region of large electronic distances is shown. Additionally, the behavior of the wave function across the turning line is seen to be reminiscent of light refraction. For weak fields, where the BO approximation does not apply, the weak-field asymptotic theory describes the spectrum accurately.
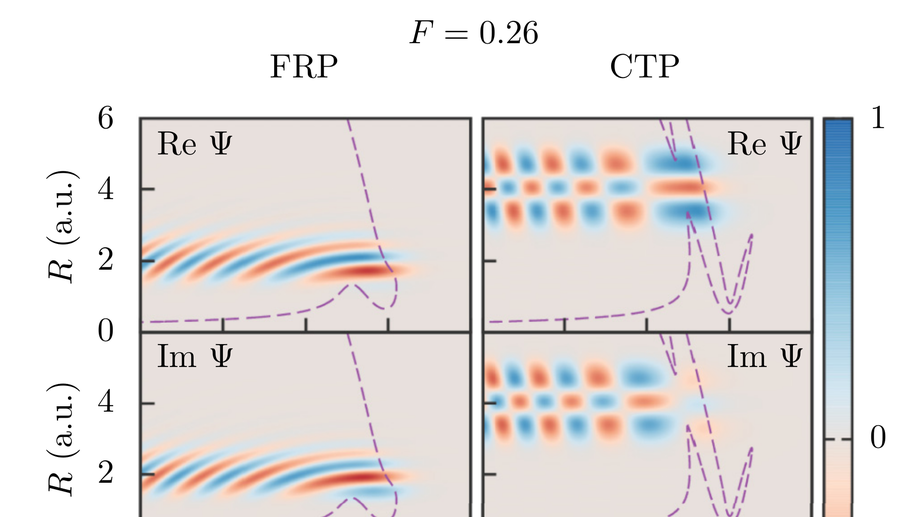
Coulomb and dipole effects in tunneling ionization of molecules including nuclear motion
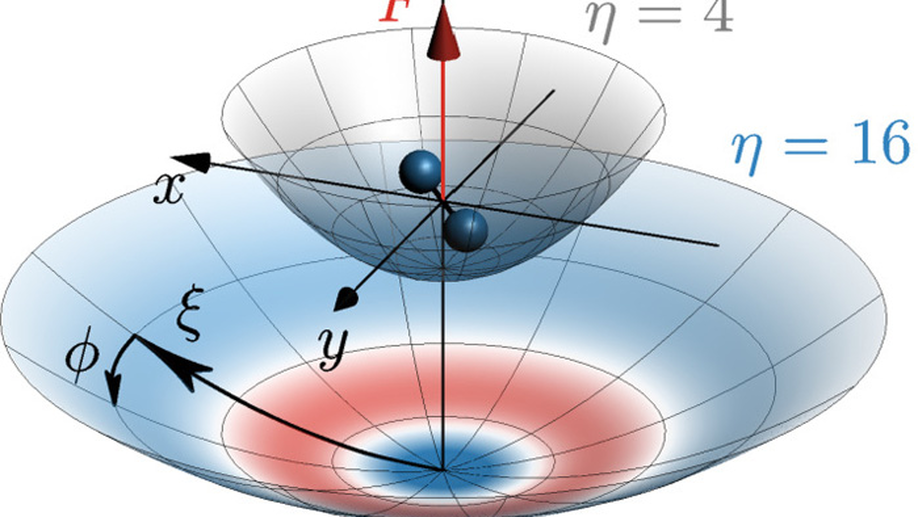
We study tunneling ionization in a one-dimensional three-body model of a molecule, treating both electronic and nuclear degrees of freedom exactly. In a recent paper [Phys. Rev. Lett. 111, 153003 (2013)] it was demonstrated using a finite-range potential that the Born-Oppenheimer approximation breaks down for fields weaker than a critical field FBO when describing tunneling ionization of molecules, but works for stronger fields. It was also demonstrated that the weak-field asymptotic theory allows for an accurate description in this weak-field limit. In the present paper, we consider a potential with a Coulomb tail and nonzero dipole moment, modeling polar molecules. Our study shows that the conclusions of the aforementioned paper also hold for this potential.